Welcome to ipysensitivityprofiler’s documentation!
Jupyter Widgets for visualizing local sensitivities of callable Python functions in a notebook.
What is a sensitivity profile?
A local sensitivity profile is the trace of a function obtained by holding all dimensions fixed but one, as shown below. It can be thought of as the intersection of a cartesian plane (in which only one input is changing) and the response surface of interest.
show code
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# Define equation
def f(x):
return -0.1 * x[0] ** 3 - 0.5 * x[1] ** 2
# Point about which to evaluate sensitivities
x0 = np.array([[1], [1]])
y0 = f(x0)
# Define bounds of design space
lb = [-5, -5] # x1_min, x2_min
ub = [ 5, 5] # x1_max, x2_max
# Grid coordinates per dimension (for plotting response surface)
resolution = 100
x1 = np.linspace(lb[0], ub[0], resolution).reshape((1, -1))
x2 = np.linspace(lb[0], ub[0], resolution).reshape((1, -1))
X1, X2 = np.meshgrid(x1, x2)
x = np.concat([X1.reshape((1, -1)), X2.reshape((1, -1))]) # flatten grid
y = f(x) # evaluate points
Y = y.reshape(X1.shape) # reshape grid
# Plot response surface
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X1, X2, Y, alpha=0.25)
# Plot profile along x1
x = np.concatenate([x1, x2])
x[1, :] = x0[1]
y = f(x)
ax.plot(x[0], x[1], y, alpha=1, color='red', linewidth=2)
# Plot profile along x2
x = np.concatenate([x1, x2])
x[0, :] = x0[0]
y = f(x)
ax.plot(x[0], x[1], y, alpha=1, color='blue', linewidth=2)
# Plot point about sensitivities are evaluated
ax.plot(x0[0], x0[1], y0, "ko")
ax.set_xlabel("x1")
ax.set_ylabel("x2")
ax.set_zlabel("y")
plt.show()
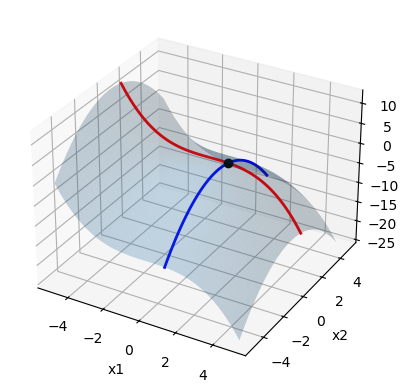
Example Usage
show code
import ipysensitivityprofiler as isp
def f(x):
return -0.1 * x[:, 0] ** 3 - 0.5 * x[:, 1] ** 2
isp.profiler(
models=[f],
xmin=[-5, -5],
xmax=[5, 5],
ymin=[-10],
ymax=[10],
x0=[1, 1],
resolution=100,
xlabels=["x1", "x2"],
ylabels=["y"],
)
Audience
The present library is intended for engineers who rely on modeling and simulation to make engineering design decisions. For example, developing physics-based or empirical models (e.g. neural net) to make predictions about some system of interest or run optimization on it.
Use Cases
Debugging models. The ability to quickly interrogate the model(s) and get instantaneous feedback goes a long way in spotting obviously wrong trends early on. This is especially helpful when developing physics-based models, before using them for optimization or design decision-making. It’s often easier to look at trends to understand what is going on, rather than infer the issue from stack error messages.
Robust design. Upon convergence, the design team might be interested in understanding how system performance would change if the design was perturbed away from nominal. This could be the result of noise in the process, requirement changes down the road, or operational uncertainty. Perturbing inputs allows engineers to verify whether system outputs would stay within desired limits based on their model(s).
Model comparison. Taking advantage of the tool’s ability to render multiple models of the same thing on the same plot, this enables two or more models to be compared against each other. For example, one model might be the high fidelity model, the other some low-fidelity version, and perhaps the third is ground truth. Provided each model has the same signature, one can very quickly observe where they disagree, as illustrated below.
show code
import ipysensitivityprofiler as isp
def f1(x):
return -0.1 * x[:, 0] ** 3 - 0.5 * x[:, 1] ** 2
def f2(x):
return -0.2 * x[:, 0] ** 3 - 0.25 * x[:, 1] ** 2
isp.profiler(
models=[f1, f2],
xmin=[-5, -5],
xmax=[5, 5],
ymin=[-10],
ymax=[10],
x0=[1, 1],
resolution=100,
xlabels=["x1", "x2"],
ylabels=["y"],
)
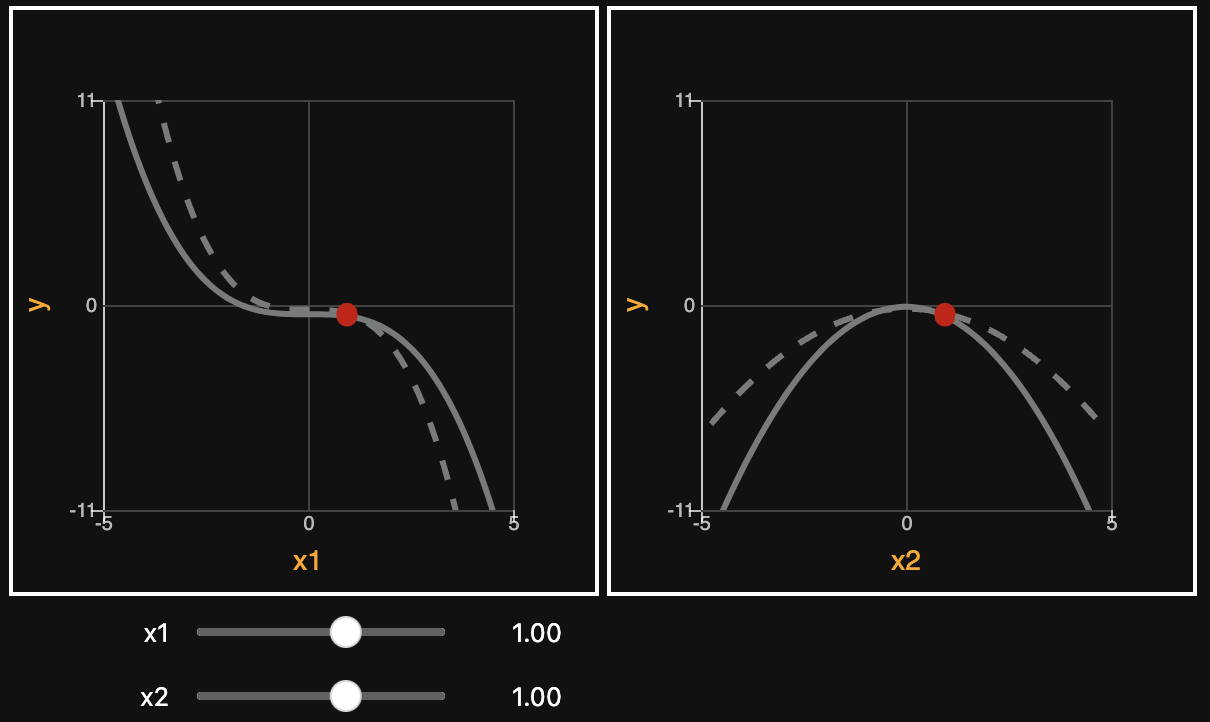
Data Structures
The response \(f\) can be any callable Python function that maps \(\boldsymbol{x}\) to \(\boldsymbol{y}\), provided it is vectorized and adopts the following signature:
where \(\boldsymbol{x}\) and \(\boldsymbol{y}\) are multidimensional arrays defined below, in which \(n_x\) is the number of inputs, \(n_y\) is the number of outputs, and \(m\) is the number of examples:
Limitations
Models must be fast for interactivity. Concretely, they must be able to evaluate thousands of datapoints on the order of milliseconds. This is a non-issue when the model at hand is some empirical regression (e.g. neural net) or even some first-order physics-based model.
The other limitation is screen realestate. This library is helpful for understanding how multiple responses and factors interact but, beyond a certain point, the number of inputs and outputs might be so big that human become overwhelmed with information and screen realestate runs out. Hence, this library is best suited for targeted studies on a subspace of a larger problem.