Welcome to jenn’s documentation!
Jacobian-Enhanced Neural Networks (JENN) are fully connected multi-layer perceptrons, whose training process is modified to predict partial derivatives accurately. This is accomplished by minimizing a modified version of the Least Squares Estimator (LSE) that accounts for Jacobian prediction error (see paper). The main benefit of jacobian-enhancement is better accuracy with fewer training points compared to standard fully connected neural nets, as illustrated below.
Example #1 |
Example #2 |
|---|---|
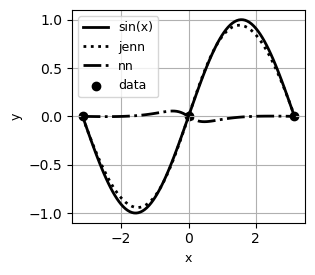
|
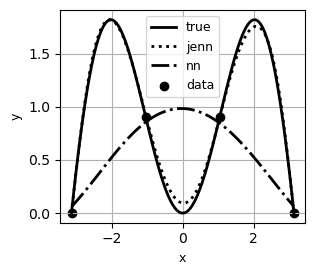
|
Example #3 |
|---|
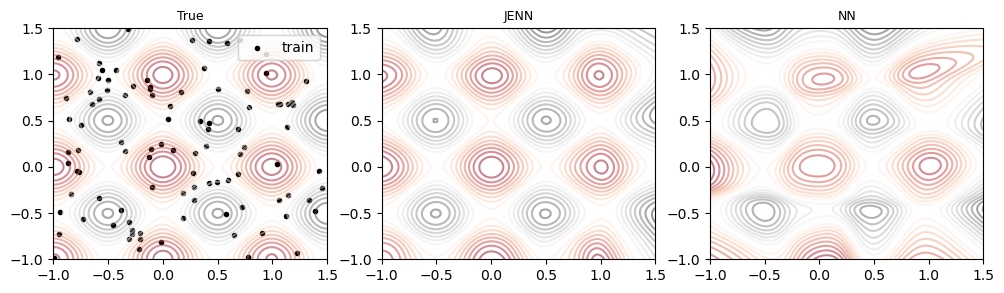
|
Audience
There exist many excellent deeplearning frameworks, such as tensorflow, which are more flexible and more performant than jenn, as well as many all-purpose ML libraries such as scikit-learn. However, gradient-enhancement is not inherently part of them and requires significant effort to be implemented in those tools. The present library is intended for those engineers in a rush with a need to predict partials accurately and who are seeking a minimal-effort API with a low-barrier to entry. Note that genn from the smt project uses jenn under-the-hood.
Use Case
JENN is intended for the field of computer aided design, where there is often a need to replace computationally expensive, physics-based models with so-called surrogate models in order to save time down the line. Since the surrogate model emulates the original model accurately in real time, it offers a speed benefit that can be used to carry out orders of magnitude more function calls quickly, opening the door to Monte Carlo simulation of expensive functions for example.
In general, the value proposition of a surrogate is that the computational expense of generating training data to fit the model is much less than the computational expense of performing the analysis with the original physics-based model itself. However, in the special case of gradient-enhanced methods, there is the additional value proposition that partials are accurate which is a critical property for one important use-case: surrogate-based optimization. The field of aerospace engineering is rich in applications of such a use-case.
Runtime
The algorithm was verified to scale as \(\mathcal{O}(n)\) using this notebook, as shown below.
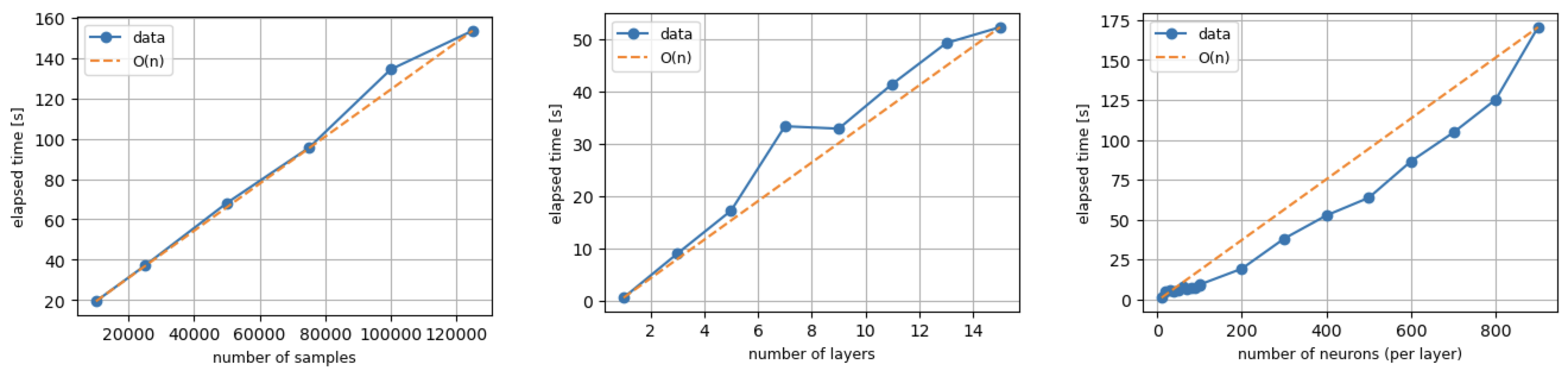
Limitations
Gradient-enhanced methods require responses to be continuous and smooth, but they are only beneficial if the cost of obtaining partials is not excessive in the first place (e.g. adjoint methods), or if the need for accuracy outweighs the cost of computing the partials. Users should therefore carefully weigh the benefit of gradient-enhanced methods relative to the needs of their application.
Acknowledgements
This code used the exercises by Prof. Andrew Ng in the Coursera Deep Learning Specialization as a starting point. It then built upon it to include additional features such as line search and plotting but, most of all, it fundamentally changed the formulation to include gradient-enhancement and made sure all arrays were updated in place (data is never copied). The author would like to thank Andrew Ng for offering the fundamentals of deep learning on Coursera, which took a complicated subject and explained it in simple terms that even an aerospace engineer could understand.