1. Installation

The core algorithm is written in Python 3. It requires numpy for computations, orjson, jsonpointer and jsonschema for serialization, and matplotlib for visualization:

pip install jenn

2. Data Structures

In order to use the library effectively, it is essential to understand its data structures. Mathematically, JENN is used to predict smooth, continuous functions of the form:

\[\boldsymbol{y} = f(\boldsymbol{x}) \qquad \Rightarrow \qquad \dfrac{\partial \boldsymbol{y}}{\partial \boldsymbol{x}} = f'(\boldsymbol{x})\]

where \(\frac{\partial \boldsymbol{y}}{\partial \boldsymbol{x}}\) is the Jacobian. For a single example, the associated quantities are given by:

\[\begin{split}\boldsymbol{x} = \left( \begin{matrix} x_1 \\ \vdots \\ x_{n_x} \end{matrix} \right) \in \mathbb{R}^{n_x} \quad \boldsymbol{y} = \left( \begin{matrix} y_1 \\ \vdots \\ y_{n_y} \end{matrix} \right) \in \mathbb{R}^{n_y} \quad \frac{\partial \boldsymbol{y}}{\partial \boldsymbol{x}} = \left( \begin{matrix} \frac{\partial y_1}{\partial x_1} & \dots & \frac{\partial y_1}{\partial x_{n_x}} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_{n_y}}{\partial x_1} & \dots & \frac{\partial y_{n_y}}{\partial x_{n_x}} \\ \end{matrix} \right) \in \mathbb{R}^{n_y \times n_x}\end{split}\]

For multiple examples, denoted by \(m\), these quantities become vectorized as follows:

\[\begin{split}\boldsymbol{X} = \left( \begin{matrix} x_1^{(1)} & \dots & x_1^{(m)} \\ \vdots & \ddots & \vdots \\ x_{n_x}^{(1)} & \dots & x_{n_x}^{(m)} \\ \end{matrix} \right) \in \mathbb{R}^{n_x \times m} \qquad \boldsymbol{Y} = \left( \begin{matrix} y_1^{(1)} & \dots & y_1^{(m)} \\ \vdots & \ddots & \vdots \\ y_{n_y}^{(1)} & \dots & y_{n_y}^{(m)} \\ \end{matrix} \right) \in \mathbb{R}^{n_y \times m}\end{split}\]

Similarly, the vectorized version of the Jacobian becomes:

\[\begin{split}\boldsymbol{J} = \left[ \begin{matrix} {\left[ \begin{matrix} \dfrac{\partial y_1}{\partial x_1}^{(1)} & \dots & \dfrac{\partial y_1}{\partial x_{1}}^{(m)} \\ \vdots & \ddots & \vdots \\ \dfrac{\partial y_{1}}{\partial x_{n_x}}^{(1)} & \dots & \dfrac{\partial y_{1}}{\partial x_{n_x}}^{(m)} \\ \end{matrix} \right]} \\ \vdots \\ {\left[ \begin{matrix} \dfrac{\partial y_{n_y}}{\partial x_1}^{(1)} & \dots & \dfrac{\partial y_{n_y}}{\partial x_{1}}^{(m)} \\ \vdots & \ddots & \vdots \\ \dfrac{\partial y_{n_y}}{\partial x_{n_x}}^{(1)} & \dots & \dfrac{\partial y_{n_y}}{\partial x_{n_x}}^{(m)} \\ \end{matrix} \right]} \end{matrix} \right] \in \mathbb{R}^{n_y \times n_x \times m}\end{split}\]

Programmatically, these data structures are exclusively represented using shaped numpy arrays:

import numpy as np

# p = number of inputs
# K = number of outputs
# m = number of examples in dataset

x = np.array(
[
   [11, 12, 13, 14],
   [21, 22, 23, 24],
   [31, 32, 33, 34],
]
)  # array of shape (n_x, m) = (3, 4)

y = np.array(
[
   [11, 12, 13, 14],
   [21, 22, 23, 24],
]
)  # array of shape (n_y, m) = (2, 4)

dydx = np.array(
[
   [
      [111, 112, 113, 114],
      [121, 122, 123, 124],
      [131, 132, 133, 134],
   ],
   [
      [211, 212, 213, 214],
      [221, 222, 223, 224],
      [231, 232, 233, 234],
   ]
]
)  # array of shape (n_y, n_x, m) = (2, 3, 4)

p, m = x.shape
K, m = y.shape
K, p, m = dydx.shape

assert y.shape[0] == dydx.shape[0]
assert x.shape[0] == dydx.shape[1]
assert x.shape[-1] == y.shape[-1] == dydx.shape[-1]

3. Usage

This section provides a quick example to get started. Consider the task of fitting a simple 1D sinusoid using only three data points:

import numpy as np
import jenn


#########################
# Example Test Function #
#########################

def f(x):
    """Compute response."""
    return np.sin(x)


def f_prime(x):
    """Compute partials."""
    return np.cos(x).reshape((1, 1, -1))  # note: jacobian adds a dimension


##########################
# Generate Training Data #
##########################

x_train = np.linspace(-np.pi , np.pi, 3).reshape((1, -1))
y_train = f(x_train)
dydx_train = f_prime(x_train)


######################
# Generate Test Data #
######################

x_test = np.linspace(-np.pi , np.pi, 30).reshape((1, -1))
y_test = f(x_test)
dydx_test = f_prime(x_test)


##################
# Fit Regular NN #
##################

regular_model = jenn.NeuralNet(
    layer_sizes=[x_train.shape[0], 3, 3, y_train.shape[0]]  # note: user defines hidden layer architecture
    ).fit(
        x_train, y_train, random_state=123  # see docstr for full list of hyperparameters
    )


############
# Fit JENN #
############

enhanced_model = jenn.NeuralNet(
    layer_sizes=[x_train.shape[0], 3, 3, y_train.shape[0]],  # note: user defines hidden layer architecture
    ).fit(
        x_train, y_train, dydx_train, random_state=123  # see docstr for full list of hyperparameters
    )


####################
# Predict Response #
####################

y_pred = enhanced_model.predict(x_test)


####################
# Predict Partials #
####################

dydx_pred = enhanced_model.predict_partials(x_train)


###########################################
# Predict Response & Partials In One Step #
###########################################

y_pred, dydx_pred = enhanced_model(x_test)


# Check how well model generalizes
assert jenn.metrics.rsquare(y_pred, y_test) > 0.99
assert jenn.metrics.rsquare(dydx_pred, dydx_test) > 0.99

Saving a model for later re-use:

enhanced_model.save("parameters.json")

Reloading the parameters a previously trained model:

reloaded_model = jenn.NeuralNet.load('parameters.json')

y_reloaded, dydx_reloaded = reloaded_model(x_test)

assert np.allclose(y_reloaded, y_pred)
assert np.allclose(dydx_reloaded, dydx_pred)

4. More Examples

Elaborated demo notebooks can be found on the project repo.

5. Other features

5.1. Plotting

For convenience, plotting tools are available using matplotlib. Continuing the previous example:

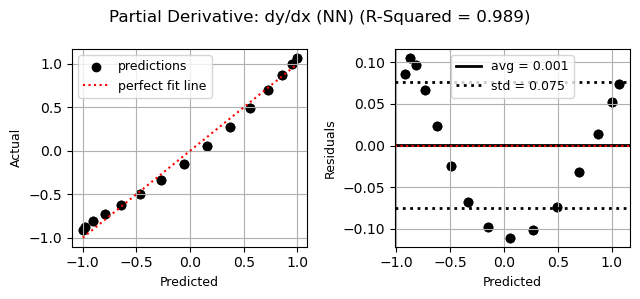
# Example: show goodness of fit of the partials
jenn.plot_goodness_of_fit(
    y_true=dydx_test,
    y_pred=enhanced_model.predict_partials(x_test),
    title="Partial Derivative: dy/dx (jenn)"
)
../_images/example_goodness_of_fit.png 
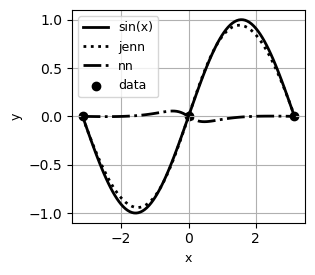
# Example: visualize local trends
jenn.plot_sensitivity_profiles(
    func=[f, enhanced_model.predict, regular_model.predict],
    x_min=x_train.min(),
    x_max=x_train.max(),
    x_true=x_train,
    y_true=y_train,
    resolution=100,
    legend_label=['sin(x)', 'jenn', 'nn'],
    xlabels=['x'],
    ylabels=['y'],
    show_cursor=False
)
../_images/example_sensitivity_profile.png

5.2. Load JMP models into Python

Not all engineers are Python enthusiasts. Sometimes, using JMP allows progress to be made fast without writing code. In fact, JMP sometimes markets their software as machine learning without code. Once a model is trained though, it often needs to be loaded into Python where it can be used in conjunction with other analyses. Here’s how to do it with JENN, where the equation is obtained using “Save Profile Formulas” in JMP:

jmp_model = jenn.utilities.from_jmp(equation="""
    6.63968579427224 + 2419.53609389846 * TanH(
        0.5 * (1.17629679110012 + -0.350827466968853 * :x1 + -0.441135986242386 * :x2)
    ) + 926.302874298947 * TanH(
        0.5 * (0.0532227576798577 + 0.112094306256208 * :x1 + -0.589518737153198 * :x2)
    ) + -4868.09413385432 * TanH(
        0.5 * (0.669012936934124 + -0.354310015265324 * :x1 + -0.442508530947179 * :x2)
    ) + 364.826302675917 * TanH(
        0.5 * (0.181903867225405 + -0.400769569147237 * :x1 + -1.82765795570436 * :x2)
    ) + 69.1044173973596 * TanH(
        0.5 * ((-1.33806951259538) + 5.05831585102242 * :x1 + 0.0768855196783658 * :x2)
    ) + 1003.55161311844 * TanH(
        0.5 * (0.333506711905318 + -1.21092868596007 * :x1 + -0.094803759612578 * :x2)
    ) + -105.644746963426 * TanH(
        0.5 * (0.0582830223989066 + -0.758691194673338 * :x1 + 0.193686573458068 * :x2)
    ) + 28.9924537808578 * TanH(
        0.5 * (1.68489056740589 + 0.203695375799704 * :x1 + 1.55265433664034 * :x2)
    ) + -16.1485832676648 * TanH(
        0.5 * (0.20830843078032 + 0.293819116867659 * :x1 + -3.34453047341792 * :x2)
    ) + -40.871646830766 * TanH(
        0.5 * (1.94906272051484 + -0.446838471653994 * :x1 + -7.96896877293616 * :x2)
    ) + 2.01890616631764 * TanH(
        0.5 * (0.501220953175385 + 1.35505831134419 * :x1 + -0.618548650974262 * :x2)
    ) + 150.412884466318 * TanH(
        0.5 * (2.21033919158451 + -0.696779972041321 * :x1 + -1.69376087699982 * :x2)
    )
""")
y, dy_dx = jmp_model(x=np.array([[0.5], [0.25]]))